Research Details - Mushfiqur Rahman Fahim

TiO₂ - water nanofluid

Progress so far

In this project, TiO₂-Water nanofluid is flown through a double pipe counter flow heat exchanger as a cooling agent to investigate the heat transfer coefficient of the nanofluid. The flow is simulated as a single phase flow for the ease of calculation. We will be simulating multiphase flow to find the effect of phase on the computational modeling of nanofluid.

First, to validate our model, 0.2% nanoparticle concentration is used in the nanofluid, as it has been done in the experimental work of Duangthongsuk and Wongwises [1]

Then, effects of reynolds number i.e. mass flow rate of the nanofluid along with the effects of different concertration will be tested in this work. Duangthongsuk and Wongwises [1] didn't investigate the effects of particle concentration in the nanofluid.

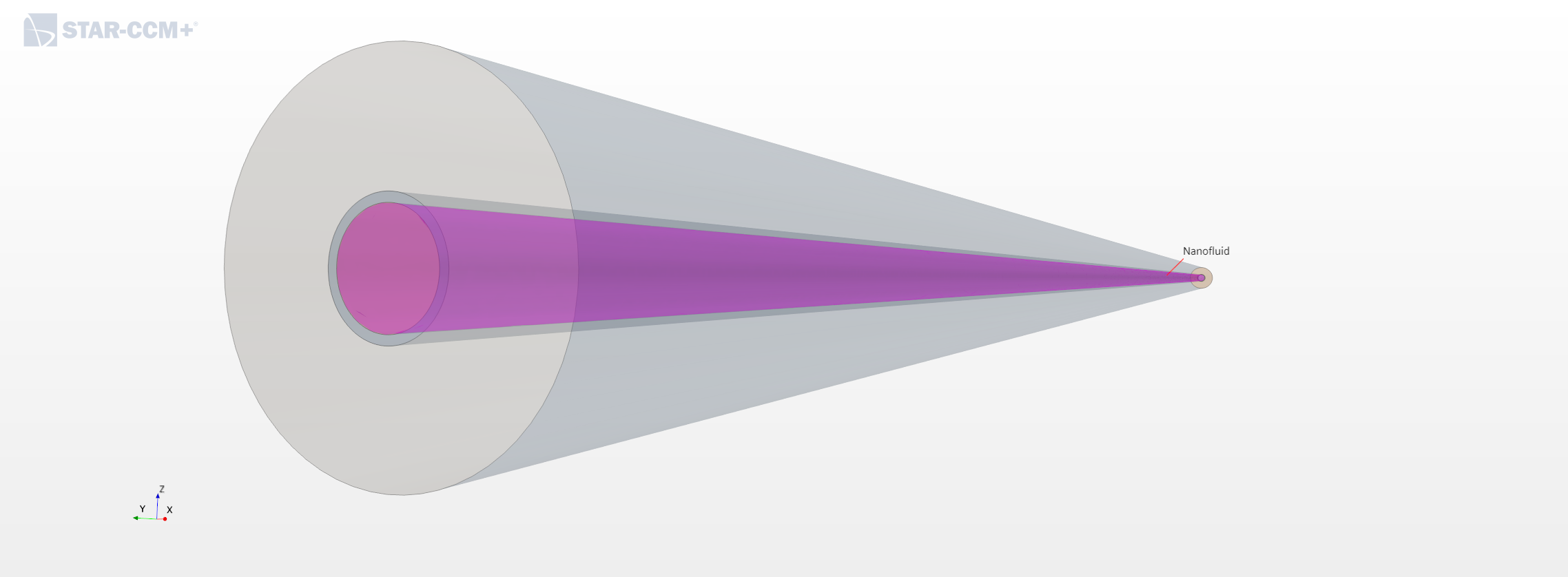
Flow domain

The flow domain consists of three regions. First, the inner side of a copper pipe through which the nanofluid will flow. The copper itself is another region, which will be a solid region. The last region will be another pipe covering the copper pipe through which the hot fluid i.e. water will flow.

The copper pipe has an inner diameter of 8.13 mm and an outer diameter of 9.53 mm. The outer pipe has a diameter of 27.8 mm.

Inlet of nanofluid and inlet of hot water are in opposite side

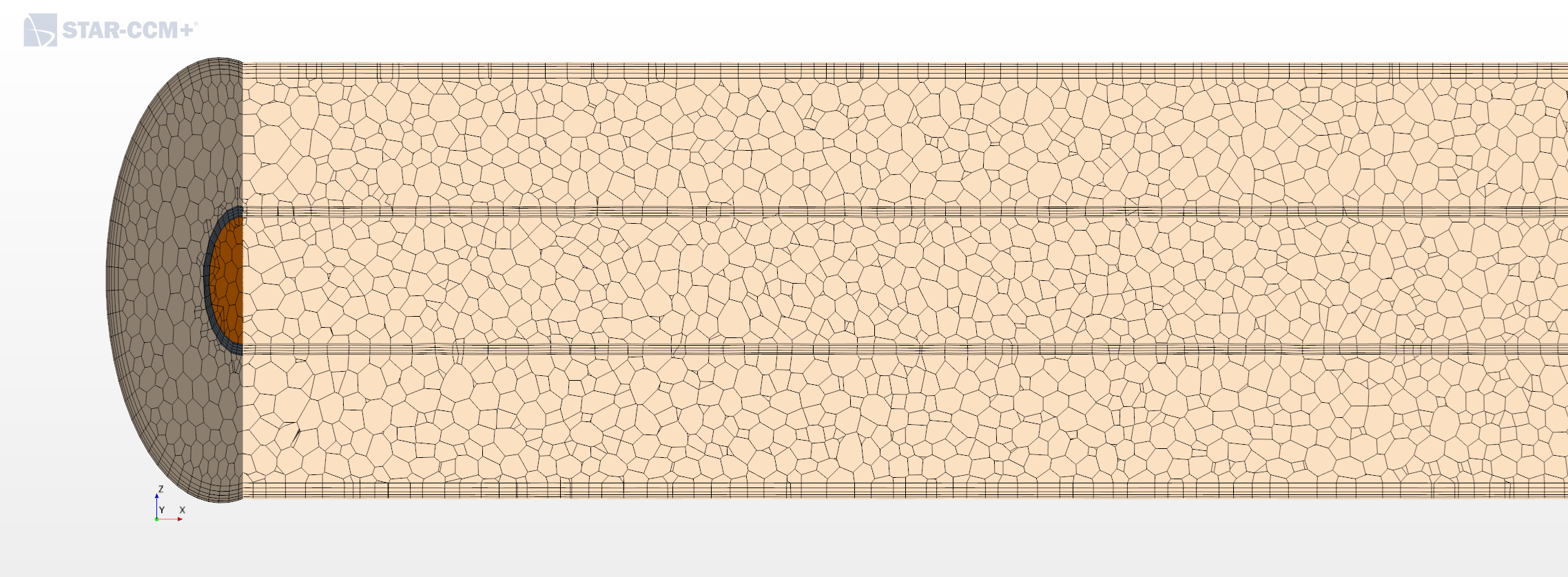
Mesh models

Surface remesher.
polyhedral for volume meshing.
Thin mesher.
Cylinder extrude mesher.
Prism layer mesher.

Cross section of mesh. Thin mesher is used for the thin copper pipe.

Residual shows a well converged solution. Where all of them are less than 10E-04 magnitude.

Nanofluid properties

Nano Particle concentration	Density (kg/m³)	Viscosity (pa-s)	Specific Heat (J/kg-K)	Thermal Conductivity (W/m-K)	Prandtl Number
0.2%	1004.09	8.93E-04	4152.11	0.6242	5.94
0.45%	1012.24	8.99E-04	4115.63	0.6293	5.88
0.6%	1017.14	9.02E-04	4094.03	0.6323	5.84
1%	1030.19	9.11E-04	4037.41	0.6404	5.74

Material properties are calculated using following equations.

Results

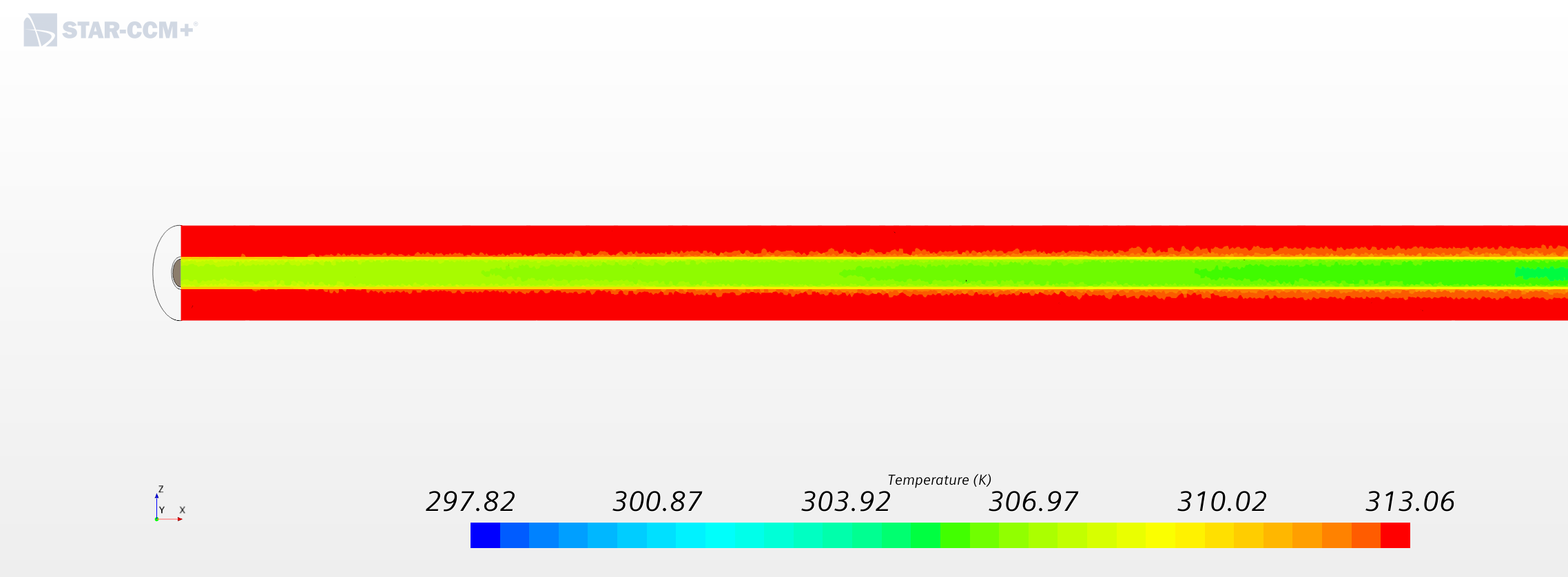
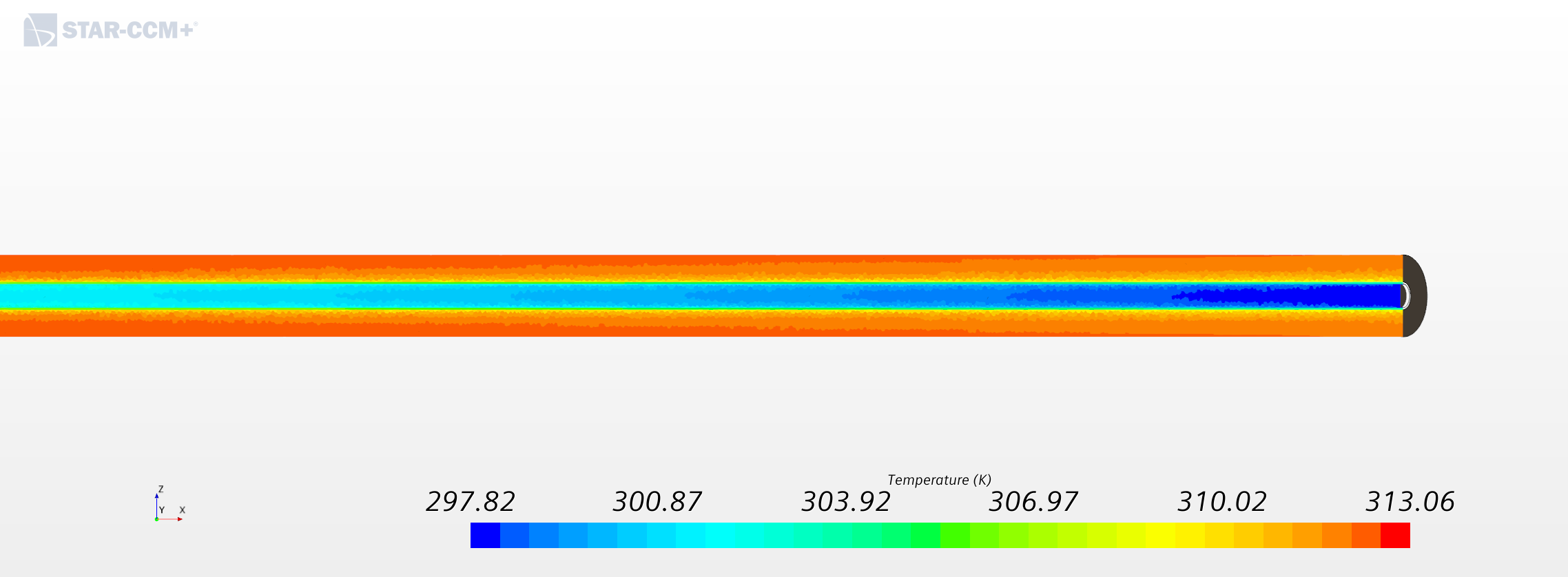
Temperature distribution at nanofluid outlet and hot water inlet.

Temperature distribution at nanofluid inlet and hot water outlet. (Decreasing blue shade towards left indicate nanofluid temperature is increasing)

Finally, the are calculated using following equations.

Heat flux of nanofluid is calculated using the classic heat transfer equation.
Q_nf=m_nfC_p.nf(T_out - T_out)
Heat flux of hot water is calculated using the classic heat transfer equation.
Q_w=m_wC_p.w(T_out - T_out)
Then their average is calcualted.
Q_avg=(Q_nf+Q_w)/2

Then the heat transfer coefficient is calculated using LMTD eqwuation.

Overall heat transfer coefficient is found to be 5.64+04 W/m²-K